Torres de Hanoi: recursividad, explicación del algoritmo y ejemplos

Las Torres de Hanoi son uno de los rompecabezas matemáticos más conocidos, pero también uno de los mejores algoritmos para entender la recursividad de forma intuitiva. En este artículo verás todo ello.

3️⃣ Dificultad: intermedia, orientado especialmente a estudiantes de desarrollo o programación que ya tienen un cierto nivel.

Este artículo sobre las torres de Hanoi, vamos a explicar el algoritmo en profundidad para que lo aprendas sin problemas y además te provea de una muy buena comprensión de la recursividad que es, al fin y al cabo, en lo que se basa este algoritmo y es uno de los pilares de la programación.

¿En qué consiste el problema de las torres de Hanoi?

Realmente, se trata de un juego matemático cuyas reglas son muy simples:

1. Disponemos de tres postes y varios discos (variable en número) cuyo diámetro es decreciente.
2. Los discos se apilan al principio, desde el más grande al más pequeño en uno de los postes, normalmente, el primero.
3. Tenemos que llevar todos los discos a otro poste vacío, normalmente al tercero o más a la derecha.
4. Sólo podemos mover un disco cada vez.
5. No podemos colocar un disco grande sobre uno pequeño.
6. Solamente se puede mover el disco que se encuentre arriba, en el poste en el que esté.

A pesar de la sencillez de sus reglas, resolverlo eficientemente requiere pensar de forma recursiva. Sin embargo, tengamos en cuenta que, como casi siempre en programación, disponemos de varias estrategias para llegar a la solución.

Recursividad: el corazón del algoritmo

No es el objetivo de este artículo el explicar la recursividad. En consecuencia y para quien no lo tenga del todo claro: la recursividad es básicamente cuando una función se llama o ejecuta a sí misma mientras que se cumpla una condición.

Pero comencemos a explicar el algoritmo. En primer lugar, llamaremos a los postes:

• Origen.
• Destino.
• Auxiliar.

Si tenemos X discos, el problema se resuelve así:

1. Mover los X−1 discos desde Auxiliar ➡️ Destino.
2. Mover los X−1 discos superiores desde Origen ➡️ Auxiliar.
3. Mover el disco más grande desde Origen ➡️ Destino.

Por supuesto es el sistema típico con bastante toque técnico que describe perfectamente lo que hay que hacer pero, no es lo más claro parar entenderlo.

Ejemplo comparativo para una mejor comprensión

Hagamos mejor un símil, una comparación con algo del mundo real. Supongamos que tenemos una obra, una construcción. Hay tres puntos donde se pueden formar pilas de sacos de cemento. El primer punto es donde ahora mismo están todos los sacos de cemento. Llamemos a este punto: A.

Acabamos de terminar de construir en el punto y tenemos que llevar la pila de sacos a un lugar o punto final donde podemos formar otra pila de sacos para que no estén tan lejos ya que hay que seguir construyendo ahí. Lo llamaremos punto C.

Como está un poco lejos, haremos uso de un punto intermedio para descansar. Lo llamaremos punto B. Dicho esto y recapitulando, tenemos:

• Punto A donde está actualmente la pila de sacos de cemento.
• Punto B donde está el punto intermedio para descansar.
• Y punto C que es el lugar donde finalmente tienen que ir todos los sacos apilados para continuar ahí la obra o construcción.

Cada saco tiene un tamaño diferente para utilizar según las necesidades y para que la pila no se caiga teniendo una buena base con el saco más grande, para evitar que las pilas se caigan, siempre tienen que quedar debajo los sacos más grandes.

Imaginemos que son 7 sacos y pedimos a los trabajadores que los muevan, teniendo cuidado de dejar siempre los sacos, desde los más grandes a los pequeños en la pila, para que ésta no se caiga. Por tanto, mueven seis sacos de A a B, y el último (el más grande que está en A), lo llevan directamente a C para que comience la pila final con una buena base.

Después tienen que ir repitiendo el proceso, dejando siempre los más grandes debajo para que la pila de sacos sea estable y no se caiga.

Ahí está la recursividad, tienen que mover siempre los sacos menores a otro lugar, dejando libres los mayores para llevarlos al punto final o C. Y eso se repetirá, hasta que se termine formando una pila de todos los sacos en C.

🎓 Adicionalmente, agreguemos un dato

El número de movimientos es:

Visualización del algoritmo

📘 🤔 ¿Quieres ampliar lo que acabas de leer? Busca más lecciones, guías y recursos en nuestro portal

Implementación del algoritmo en diferentes lenguajes 👨‍💻

Es importante tener en cuenta que podemos resolver este problema de las torres de Hanoi de varias formas, dependiendo de cómo se aborde y cómo queramos mostrarlo (estamos hablando de un programa no de un juego de mesa, ahora).

En consecuencia, obviamente usaremos las reglas del juego pero la situación será, que pedimos al usuario cuántos discos están en el primer poste y al final, se moverán todos los discos al tercer poste. Por tanto, el diagrama de flujo, el Nassi y el pseudocódigo son representaciones totalmente equivalentes.

Pseudocódigo

Funcion resolver_hanoi(n_discos,origen_torre,destino_torre,auxiliar_torre,torres,cant_discos,movimientos,num_movimiento)
	Definir disco Como Entero
	Si n_discos=1 Entonces
		// Mover un disco directamente
		disco <- torres[origen_torre,cant_discos[origen_torre]]
		cant_discos[origen_torre] <- cant_discos[origen_torre]-1
		cant_discos[destino_torre] <- cant_discos[destino_torre]+1
		torres[destino_torre,cant_discos[destino_torre]]<-disco
		num_movimiento <- num_movimiento+1
		Escribir 'Movimiento ',num_movimiento,': Mover disco ',disco,' de torre ',origen_torre,' a torre ',destino_torre
		// Guardar el movimiento
		movimientos[num_movimiento,1]<-origen_torre
		movimientos[num_movimiento,2]<-destino_torre
	SiNo
		// Mover n-1 discos de origen a auxiliar usando destino
		resolver_hanoi(n_discos-1,origen_torre,auxiliar_torre,destino_torre,torres,cant_discos,movimientos,num_movimiento)
		// Mover el disco mas grande de origen a destino
		disco <- torres[origen_torre,cant_discos[origen_torre]]
		cant_discos[origen_torre] <- cant_discos[origen_torre]-1
		cant_discos[destino_torre] <- cant_discos[destino_torre]+1
		torres[destino_torre,cant_discos[destino_torre]]<-disco
		num_movimiento <- num_movimiento+1
		Escribir 'Movimiento ',num_movimiento,': Mover disco ',disco,' de torre ',origen_torre,' a torre ',destino_torre
		movimientos[num_movimiento,1]<-origen_torre
		movimientos[num_movimiento,2]<-destino_torre
		// Mover n-1 discos de auxiliar a destino usando origen
		resolver_hanoi(n_discos-1,auxiliar_torre,destino_torre,origen_torre,torres,cant_discos,movimientos,num_movimiento)
	FinSi
FinFuncion

Algoritmo TorresDeHanoi
	Definir discos,i,max_movimientos,num_movimiento Como Entero
	Dimension torres[3,10]
	Dimension cant_discos[3]
	Dimension movimientos[300,2]
	// Pedir cantidad de discos
	Escribir 'Ingrese el numero de discos (1-8):'
	Leer discos
	Mientras discos<1 O discos>8 Hacer
		Escribir 'El numero de discos debe ser entre 1 y 8:'
		Leer discos
	FinMientras
	// Inicializar las torres
	cant_discos[1] <- discos
	cant_discos[2] <- 0
	cant_discos[3] <- 0
	Para i<-1 Hasta discos Hacer
		torres[1,i]<-i
	FinPara
	Escribir ''
	Escribir 'Estado inicial:'
	Escribir 'Torre 1: ',discos,' discos'
	Escribir 'Torre 2: vacia'
	Escribir 'Torre 3: vacia'
	Escribir ''
	Escribir 'Resolviendo...'
	Escribir ''
	// Resolver
	num_movimiento <- 0
	resolver_hanoi(discos,1,3,2,torres,cant_discos,movimientos,num_movimiento)
	// Calcular total de movimientos esperados
	max_movimientos <- 1
	Para i<-1 Hasta discos Hacer
		max_movimientos <- max_movimientos*2
	FinPara
	max_movimientos <- max_movimientos-1
	Escribir ''
	Escribir 'Problema resuelto en ',num_movimiento,' movimientos'
	Escribir 'Movimientos teoricos minimos: ',max_movimientos
	Escribir ''
	Escribir 'Estado final:'
	Escribir 'Torre 1: ',cant_discos[1],' discos'
	Escribir 'Torre 2: ',cant_discos[2],' discos'
	Escribir 'Torre 3: ',cant_discos[3],' discos'
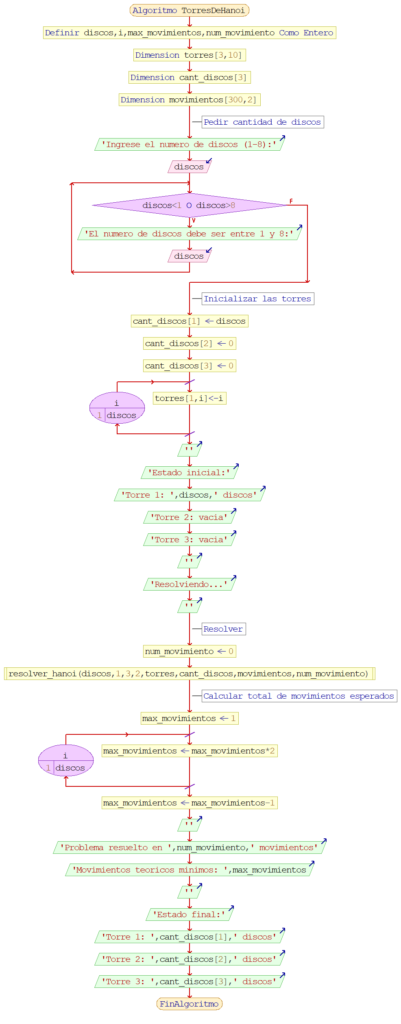
FinAlgoritmo

Diagrama de flujo

Tal y como hemos indicado, los diagramas van totalmente acorde al pseudocódigo, así que disponemos de dos diagramas, uno para la función resolver_hanoi() y otro para el algoritmo principal, TorresDeHanoi.

La función resolver_hanoi():

El algoritmo principal TorresDeHanoi:

Nassi–Shneiderman

Seguidamente, mostremos ahora el Nassi-Shneiderman correspondiente, tanto de la función resolver_hanoi() como del algoritmo principal.

Función resolver_hanoi():

Algoritmo principal TorresDeHanoi:

A continuación, mostraremos la implementación del algoritmo de resolución del problema de Torres de Hanoi, por recursividad. El código indicado por supuesto, depende de cada lenguaje de programación y no sigue el pseudocódigo expuesto en cada detalle, pero sí en la idea principal.

📘 🤔 ¿Quieres ampliar lo que acabas de leer? Busca más lecciones, guías y recursos en nuestro portal

C

Tal y como he indicado más arriba, el pseudocódigo (y los diagramas correspondientes), están creados con un objetivo pedagógico. Los siguientes ejemplos en diferentes lenguajes (incluyendo este de C), también lo hacen pero, aunque aplican el algoritmo recursivo, lo hacen con detalles diferentes al pseudocódigo de más arriba. Ya que cada lenguaje tiene sus características, encuentro más útil realizarlo así, y de paso, se ven diferentes posibilidades con un mismo algoritmo. De hecho, recomiendo un sencillo ejercicio: adaptar el pseudocódigo al 100% a los diferentes lenguajes que os interesen.

#include <stdio.h>
#include <math.h>

// Contador global de movimientos
int contador_movimientos = 0;

void hanoi(int n, char origen, char destino, char auxiliar) {
    if (n == 1) {
        contador_movimientos++;
        printf("Movimiento %d: Mover disco 1 de torre %c a torre %c\n", 
               contador_movimientos, origen, destino);
        return;
    }
    
    // Mover n-1 discos de origen a auxiliar usando destino
    hanoi(n - 1, origen, auxiliar, destino);
    
    // Mover el disco más grande de origen a destino
    contador_movimientos++;
    printf("Movimiento %d: Mover disco %d de torre %c a torre %c\n", 
           contador_movimientos, n, origen, destino);
    
    // Mover n-1 discos de auxiliar a destino usando origen
    hanoi(n - 1, auxiliar, destino, origen);
}

int main() {
    int num_discos;
    int movimientos_teoricos;
    
    printf("===========================================\n");
    printf("   TORRES DE HANOI - Solucion Recursiva\n");
    printf("===========================================\n\n");
    
    // Solicitar número de discos
    printf("Introduce el numero de discos (recomendado 1-10): ");
    scanf("%d", &num_discos);
    
    // Validación
    if (num_discos < 1) {
        printf("Error: El numero de discos debe ser al menos 1.\n");
        return 1;
    }
    
    if (num_discos > 15) {
        printf("Advertencia: Con %d discos habra %d movimientos.\n", 
               num_discos, (int)pow(2, num_discos) - 1);
        printf("¿Deseas continuar? (s/n): ");
        char respuesta;
        scanf(" %c", &respuesta);
        if (respuesta != 's' && respuesta != 'S') {
            printf("Programa terminado.\n");
            return 0;
        }
    }
    
    // Mostrar información inicial
    printf("\nEstado inicial:\n");
    printf("  Torre A: %d disco(s)\n", num_discos);
    printf("  Torre B: vacia (auxiliar)\n");
    printf("  Torre C: vacia (destino)\n\n");
    
    printf("Objetivo: Mover todos los discos de A a C\n");
    printf("Reglas: \n");
    printf("  1. Solo se puede mover un disco a la vez\n");
    printf("  2. Un disco grande nunca sobre uno pequeno\n\n");
    
    printf("-------------------------------------------\n");
    printf("Secuencia de movimientos:\n");
    printf("-------------------------------------------\n");
    
    // Resolver las Torres de Hanoi
    hanoi(num_discos, 'A', 'C', 'B');
    
    // Calcular movimientos teóricos mínimos
    movimientos_teoricos = (int)pow(2, num_discos) - 1;
    
    // Mostrar resumen
    printf("\n===========================================\n");
    printf("RESUMEN:\n");
    printf("===========================================\n");
    printf("Total de movimientos realizados: %d\n", contador_movimientos);
    printf("Movimientos minimos teoricos:    %d\n", movimientos_teoricos);
    printf("\nEstado final:\n");
    printf("  Torre A: vacia\n");
    printf("  Torre B: vacia\n");
    printf("  Torre C: %d disco(s)\n", num_discos);
    printf("\nProblema resuelto correctamente!\n");
    printf("===========================================\n");
    
    return 0;
}

C++

#include <iostream>
#include <cmath>
#include <string>

using namespace std;

// Contador global de movimientos
int contador_movimientos = 0;

void hanoi(int n, char origen, char destino, char auxiliar) {
    if (n == 1) {
        contador_movimientos++;
        cout << "Movimiento " << contador_movimientos 
             << ": Mover disco 1 de torre " << origen 
             << " a torre " << destino << endl;
        return;
    }
    
    // Mover n-1 discos de origen a auxiliar usando destino
    hanoi(n - 1, origen, auxiliar, destino);
    
    // Mover el disco más grande de origen a destino
    contador_movimientos++;
    cout << "Movimiento " << contador_movimientos 
         << ": Mover disco " << n << " de torre " << origen 
         << " a torre " << destino << endl;
    
    // Mover n-1 discos de auxiliar a destino usando origen
    hanoi(n - 1, auxiliar, destino, origen);
}

int main() {
    int num_discos;
    int movimientos_teoricos;
    
    cout << "===========================================" << endl;
    cout << "   TORRES DE HANOI - Solucion Recursiva" << endl;
    cout << "===========================================" << endl << endl;
    
    // Solicitar número de discos
    cout << "Introduce el numero de discos (recomendado 1-10): ";
    cin >> num_discos;
    
    // Validación
    if (num_discos < 1) {
        cout << "Error: El numero de discos debe ser al menos 1." << endl;
        return 1;
    }
    
    if (num_discos > 15) {
        cout << "Advertencia: Con " << num_discos << " discos habra " 
             << (int)pow(2, num_discos) - 1 << " movimientos." << endl;
        cout << "¿Deseas continuar? (s/n): ";
        char respuesta;
        cin >> respuesta;
        if (respuesta != 's' && respuesta != 'S') {
            cout << "Programa terminado." << endl;
            return 0;
        }
    }
    
    // Mostrar información inicial
    cout << endl << "Estado inicial:" << endl;
    cout << "  Torre A: " << num_discos << " disco(s)" << endl;
    cout << "  Torre B: vacia (auxiliar)" << endl;
    cout << "  Torre C: vacia (destino)" << endl << endl;
    
    cout << "Objetivo: Mover todos los discos de A a C" << endl;
    cout << "Reglas: " << endl;
    cout << "  1. Solo se puede mover un disco a la vez" << endl;
    cout << "  2. Un disco grande nunca sobre uno pequeno" << endl << endl;
    
    cout << "-------------------------------------------" << endl;
    cout << "Secuencia de movimientos:" << endl;
    cout << "-------------------------------------------" << endl;
    
    // Resolver las Torres de Hanoi
    hanoi(num_discos, 'A', 'C', 'B');
    
    // Calcular movimientos teóricos mínimos
    movimientos_teoricos = (int)pow(2, num_discos) - 1;
    
    // Mostrar resumen
    cout << endl << "===========================================" << endl;
    cout << "RESUMEN:" << endl;
    cout << "===========================================" << endl;
    cout << "Total de movimientos realizados: " << contador_movimientos << endl;
    cout << "Movimientos minimos teoricos:    " << movimientos_teoricos << endl;
    cout << endl << "Estado final:" << endl;
    cout << "  Torre A: vacia" << endl;
    cout << "  Torre B: vacia" << endl;
    cout << "  Torre C: " << num_discos << " disco(s)" << endl;
    cout << endl << "Problema resuelto correctamente!" << endl;
    cout << "===========================================" << endl;
    
    return 0;
}

Java

import java.util.Scanner;

public class TorresDeHanoi {
    
    // Contador global de movimientos
    private static int contadorMovimientos = 0;
    
    public static void hanoi(int n, char origen, char destino, char auxiliar) {
        if (n == 1) {
            contadorMovimientos++;
            System.out.println("Movimiento " + contadorMovimientos 
                + ": Mover disco 1 de torre " + origen 
                + " a torre " + destino);
            return;
        }
        
        // Mover n-1 discos de origen a auxiliar usando destino
        hanoi(n - 1, origen, auxiliar, destino);
        
        // Mover el disco más grande de origen a destino
        contadorMovimientos++;
        System.out.println("Movimiento " + contadorMovimientos 
            + ": Mover disco " + n + " de torre " + origen 
            + " a torre " + destino);
        
        // Mover n-1 discos de auxiliar a destino usando origen
        hanoi(n - 1, auxiliar, destino, origen);
    }
    
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int numDiscos;
        int movimientosTeoricos;
        
        System.out.println("===========================================");
        System.out.println("   TORRES DE HANOI - Solucion Recursiva");
        System.out.println("===========================================\n");
        
        // Solicitar número de discos
        System.out.print("Introduce el numero de discos (recomendado 1-10): ");
        numDiscos = scanner.nextInt();
        
        // Validación
        if (numDiscos < 1) {
            System.out.println("Error: El numero de discos debe ser al menos 1.");
            scanner.close();
            return;
        }
        
        if (numDiscos > 15) {
            System.out.println("Advertencia: Con " + numDiscos + " discos habra " 
                + ((int)Math.pow(2, numDiscos) - 1) + " movimientos.");
            System.out.print("¿Deseas continuar? (s/n): ");
            char respuesta = scanner.next().charAt(0);
            if (respuesta != 's' && respuesta != 'S') {
                System.out.println("Programa terminado.");
                scanner.close();
                return;
            }
        }
        
        // Mostrar información inicial
        System.out.println("\nEstado inicial:");
        System.out.println("  Torre A: " + numDiscos + " disco(s)");
        System.out.println("  Torre B: vacia (auxiliar)");
        System.out.println("  Torre C: vacia (destino)\n");
        
        System.out.println("Objetivo: Mover todos los discos de A a C");
        System.out.println("Reglas:");
        System.out.println("  1. Solo se puede mover un disco a la vez");
        System.out.println("  2. Un disco grande nunca sobre uno pequeno\n");
        
        System.out.println("-------------------------------------------");
        System.out.println("Secuencia de movimientos:");
        System.out.println("-------------------------------------------");
        
        // Resolver las Torres de Hanoi
        hanoi(numDiscos, 'A', 'C', 'B');
        
        // Calcular movimientos teóricos mínimos
        movimientosTeoricos = (int)Math.pow(2, numDiscos) - 1;
        
        // Mostrar resumen
        System.out.println("\n===========================================");
        System.out.println("RESUMEN:");
        System.out.println("===========================================");
        System.out.println("Total de movimientos realizados: " + contadorMovimientos);
        System.out.println("Movimientos minimos teoricos:    " + movimientosTeoricos);
        System.out.println("\nEstado final:");
        System.out.println("  Torre A: vacia");
        System.out.println("  Torre B: vacia");
        System.out.println("  Torre C: " + numDiscos + " disco(s)");
        System.out.println("\nProblema resuelto correctamente!");
        System.out.println("===========================================");
        
        scanner.close();
    }
}

JavaScript

Dado que hoy en día, decir JavaScript es meternos con no se cuántos frameworks, versiones e historias varias, opto por indicar lo que llamamos Vanilla JavaScript (es decir, puro), orientado al navegador al 100%:

// Contador global de movimientos
let contadorMovimientos = 0;

function hanoi(n, origen, destino, auxiliar) {
    if (n === 1) {
        contadorMovimientos++;
        console.log(`Movimiento ${contadorMovimientos}: Mover disco 1 de torre ${origen} a torre ${destino}`);
        return;
    }
    
    // Mover n-1 discos de origen a auxiliar usando destino
    hanoi(n - 1, origen, auxiliar, destino);
    
    // Mover el disco más grande de origen a destino
    contadorMovimientos++;
    console.log(`Movimiento ${contadorMovimientos}: Mover disco ${n} de torre ${origen} a torre ${destino}`);
    
    // Mover n-1 discos de auxiliar a destino usando origen
    hanoi(n - 1, auxiliar, destino, origen);
}

function main() {
    console.log("===========================================");
    console.log("   TORRES DE HANOI - Solucion Recursiva");
    console.log("===========================================\n");

    let respuesta = prompt("Introduce el número de discos (recomendado 1-10):");
    const numDiscos = parseInt(respuesta);

    // Validación
    if (numDiscos < 1 || isNaN(numDiscos)) {
        console.log("Error: El número de discos debe ser al menos 1.");
        return;
    }

    if (numDiscos > 15) {
        const movimientos = Math.pow(2, numDiscos) - 1;
        let confirmar = prompt(`Advertencia: Con ${numDiscos} discos habrá ${movimientos} movimientos.\n¿Deseas continuar? (s/n):`);
        if (!confirmar || confirmar.toLowerCase() !== 's') {
            console.log("Programa terminado.");
            return;
        }
    }

    ejecutarHanoi(numDiscos);
}

function ejecutarHanoi(numDiscos) {
    // Mostrar información inicial
    console.log("\nEstado inicial:");
    console.log(`  Torre A: ${numDiscos} disco(s)`);
    console.log("  Torre B: vacía (auxiliar)");
    console.log("  Torre C: vacía (destino)\n");
    
    console.log("Objetivo: Mover todos los discos de A a C");
    console.log("Reglas:");
    console.log("  1. Solo se puede mover un disco a la vez");
    console.log("  2. Un disco grande nunca sobre uno pequeño\n");
    
    console.log("-------------------------------------------");
    console.log("Secuencia de movimientos:");
    console.log("-------------------------------------------");
    
    // Resolver las Torres de Hanoi
    contadorMovimientos = 0; // Reiniciar contador
    hanoi(numDiscos, 'A', 'C', 'B');
    
    // Calcular movimientos teóricos mínimos
    const movimientosTeoricos = Math.pow(2, numDiscos) - 1;
    
    // Mostrar resumen
    console.log("\n===========================================");
    console.log("RESUMEN:");
    console.log("===========================================");
    console.log(`Total de movimientos realizados: ${contadorMovimientos}`);
    console.log(`Movimientos mínimos teóricos:    ${movimientosTeoricos}`);
    console.log("\nEstado final:");
    console.log("  Torre A: vacía");
    console.log("  Torre B: vacía");
    console.log(`  Torre C: ${numDiscos} disco(s)`);
    console.log("\n¡Problema resuelto correctamente!");
    console.log("===========================================");
}

// Ejecutar el programa automáticamente al cargar el script
main();

Python

def hanoi(n, origen, destino, auxiliar, contador):
    if n == 1:
        contador[0] += 1
        print(f"Movimiento {contador[0]}: Mover disco 1 de torre {origen} a torre {destino}")
        return
    hanoi(n - 1, origen, auxiliar, destino, contador)
    contador[0] += 1
    print(f"Movimiento {contador[0]}: Mover disco {n} de torre {origen} a torre {destino}")
    hanoi(n - 1, auxiliar, destino, origen, contador)

def main():
    print("===========================================")
    print("   TORRES DE HANOI - Solución Recursiva")
    print("===========================================\n")

    try:
        num_discos = int(input("Introduce el número de discos (recomendado 1-10): "))
    except ValueError:
        print("Error: Debes introducir un número entero.")
        return

    if num_discos < 1:
        print("Error: El número de discos debe ser al menos 1.")
        return

    if num_discos > 15:
        movimientos = 2 ** num_discos - 1
        confirmar = input(f"Advertencia: Con {num_discos} discos habrá {movimientos} movimientos.\n¿Deseas continuar? (s/n): ")
        if confirmar.lower() != 's':
            print("Programa terminado.")
            return

    print("\nEstado inicial:")
    print(f"  Torre A: {num_discos} disco(s)")
    print("  Torre B: vacía (auxiliar)")
    print("  Torre C: vacía (destino)\n")

    print("Objetivo: Mover todos los discos de A a C")
    print("Reglas:")
    print("  1. Solo se puede mover un disco a la vez")
    print("  2. Un disco grande nunca sobre uno pequeño\n")

    print("-------------------------------------------")
    print("Secuencia de movimientos:")
    print("-------------------------------------------")

    contador = [0]  # Usamos una lista para que sea mutable y se actualice en la recursión
    hanoi(num_discos, 'A', 'C', 'B', contador)

    movimientos_teoricos = 2 ** num_discos - 1

    print("\n===========================================")
    print("RESUMEN:")
    print("===========================================")
    print(f"Total de movimientos realizados: {contador[0]}")
    print(f"Movimientos mínimos teóricos:    {movimientos_teoricos}")
    print("\nEstado final:")
    print("  Torre A: vacía")
    print("  Torre B: vacía")
    print(f"  Torre C: {num_discos} disco(s)")
    print("\n¡Problema resuelto correctamente!")
    print("===========================================")

if __name__ == "__main__":
    main()

PHP

Sigamos avanzando, ahora con PHP. Eso sí, el siguiente código está orientado totalmente a consola:

<?php
// Contador global de movimientos
$contadorMovimientos = 0;

/**
 * Función recursiva para resolver el problema de las Torres de Hanói.
 *
 * @param int $n Número de discos a mover.
 * @param string $origen Torre de origen (A, B, C).
 * @param string $destino Torre de destino (A, B, C).
 * @param string $auxiliar Torre auxiliar (A, B, C).
 */
function hanoi(int $n, string $origen, string $destino, string $auxiliar)
{
    global $contadorMovimientos;

    // Caso base: si solo queda un disco, muévelo directamente
    if ($n === 1) {
        $contadorMovimientos++;
        echo "Movimiento $contadorMovimientos: Mover disco 1 de torre $origen a torre $destino\n";
        return;
    }
    
    // 1. Mover n-1 discos de origen a auxiliar usando destino
    hanoi($n - 1, $origen, $auxiliar, $destino);
    
    // 2. Mover el disco más grande (el disco n) de origen a destino
    $contadorMovimientos++;
    echo "Movimiento $contadorMovimientos: Mover disco $n de torre $origen a torre $destino\n";
    
    // 3. Mover n-1 discos de auxiliar a destino usando origen
    hanoi($n - 1, $auxiliar, $destino, $origen);
}

/**
 * Ejecuta la lógica principal del programa y muestra el resumen.
 *
 * @param int $numDiscos El número de discos con el que ejecutar el juego.
 */
function ejecutarHanoi(int $numDiscos)
{
    global $contadorMovimientos;
    
    // Reiniciar por si se ejecuta varias veces (aunque aquí solo es una)
    $contadorMovimientos = 0; 

    // Mostrar información inicial
    echo "\nEstado inicial:\n";
    echo "  Torre A: $numDiscos disco(s)\n";
    echo "  Torre B: vacia (auxiliar)\n";
    echo "  Torre C: vacia (destino)\n\n";
    
    echo "Objetivo: Mover todos los discos de A a C\n";
    echo "Reglas:\n";
    echo "  1. Solo se puede mover un disco a la vez\n";
    echo "  2. Un disco grande nunca sobre uno pequeño\n\n";
    
    echo "-------------------------------------------\n";
    echo "Secuencia de movimientos:\n";
    echo "-------------------------------------------\n";
    
    // Resolver las Torres de Hanói: Mover de 'A' a 'C' usando 'B'
    hanoi($numDiscos, 'A', 'C', 'B');
    
    // Calcular movimientos teóricos mínimos: $2^n - 1$
    $movimientosTeoricos = (2 ** $numDiscos) - 1;
    
    // Mostrar resumen
    echo "\n===========================================\n";
    echo "RESUMEN:\n";
    echo "===========================================\n";
    echo "Total de movimientos realizados: $contadorMovimientos\n";
    echo "Movimientos mínimos teóricos:     $movimientosTeoricos\n";
    echo "\nEstado final:\n";
    echo "  Torre A: vacia\n";
    echo "  Torre B: vacia\n";
    echo "  Torre C: $numDiscos disco(s)\n";
    echo "\nProblema resuelto correctamente!\n";
    echo "===========================================\n";
}

/**
 * Función principal para la interacción con el usuario en CLI.
 */
function main()
{
    echo "===========================================\n";
    echo "    TORRES DE HANOI - Solución Recursiva\n";
    echo "===========================================\n\n";
    
    // Pedir el número de discos (readline es específico de PHP CLI)
    $respuesta = readline("Introduce el número de discos (recomendado 1-10): ");
    
    $numDiscos = (int)$respuesta;
    
    // Validación
    if ($numDiscos < 1 || !is_numeric($respuesta)) {
        echo "Error: El número de discos debe ser un número entero y al menos 1.\n";
        return;
    }
    
    // Advertencia para muchos movimientos
    if ($numDiscos > 15) {
        $movimientos = (2 ** $numDiscos) - 1;
        echo "Advertencia: Con $numDiscos discos habrá $movimientos movimientos.\n";
        
        $confirmar = readline("¿Deseas continuar? (s/n): ");
        
        if (strtolower($confirmar) !== 's') {
            echo "Programa terminado.\n";
            return;
        }
    }
    
    ejecutarHanoi($numDiscos);
}

// Ejecutar el programa
main();

Kotlin

import kotlin.math.pow
import kotlin.system.exitProcess

// Variable global (o propiedad de nivel superior) para contar movimientos
var contadorMovimientos = 0

/**
 * Función recursiva para resolver el problema de las Torres de Hanói.
 * Utiliza tailrec (optimización de cola) cuando sea posible, aunque
 * la naturaleza del algoritmo de Hanói es inherentemente no-tail-recursive
 * debido a las dos llamadas recursivas posteriores a la acción central.
 *
 * @param n Número de discos a mover.
 * @param origen Torre de origen (A, B, C).
 * @param destino Torre de destino (A, B, C).
 * @param auxiliar Torre auxiliar (A, B, C).
 */
fun hanoi(n: Int, origen: Char, destino: Char, auxiliar: Char) {
    // Caso base: si solo queda un disco, muévelo directamente
    if (n == 1) {
        contadorMovimientos++
        println("Movimiento $contadorMovimientos: Mover disco 1 de torre $origen a torre $destino")
        return
    }

    // 1. Mover n-1 discos de origen a auxiliar usando destino
    hanoi(n - 1, origen, auxiliar, destino)

    // 2. Mover el disco más grande (el disco n) de origen a destino
    contadorMovimientos++
    println("Movimiento $contadorMovimientos: Mover disco $n de torre $origen a torre $destino")

    // 3. Mover n-1 discos de auxiliar a destino usando origen
    hanoi(n - 1, auxiliar, destino, origen)
}

/**
 * Ejecuta la lógica principal del problema y muestra el resumen.
 *
 * @param numDiscos El número de discos con el que ejecutar el juego.
 */
fun ejecutarHanoi(numDiscos: Int) {
    // Restablecer el contador para asegurar el inicio limpio
    contadorMovimientos = 0 

    // Mostrar información inicial
    println("\nEstado inicial:")
    println("  Torre A: $numDiscos disco(s)")
    println("  Torre B: vacía (auxiliar)")
    println("  Torre C: vacía (destino)\n")

    println("Objetivo: Mover todos los discos de A a C")
    println("Reglas:")
    println("  1. Solo se puede mover un disco a la vez")
    println("  2. Un disco grande nunca sobre uno pequeño\n")

    println("-------------------------------------------")
    println("Secuencia de movimientos:")
    println("-------------------------------------------")

    // Resolver las Torres de Hanói: Mover de 'A' a 'C' usando 'B'
    // Se usan caracteres ('A', 'C', 'B') para las torres, más idiomático en Kotlin.
    hanoi(numDiscos, 'A', 'C', 'B')

    // Calcular movimientos teóricos mínimos: 2^n - 1
    // Usamos .pow() de kotlin.math.
    val movimientosTeoricos = (2.0.pow(numDiscos) - 1).toInt()

    // Mostrar resumen
    println("\n===========================================")
    println("RESUMEN:")
    println("===========================================")
    println("Total de movimientos realizados: $contadorMovimientos")
    println("Movimientos mínimos teóricos:     $movimientosTeoricos")
    println("\nEstado final:")
    println("  Torre A: vacía")
    println("  Torre B: vacía")
    println("  Torre C: $numDiscos disco(s)")
    println("\n¡Problema resuelto correctamente!")
    println("===========================================")
}

/**
 * Función principal para la interacción con el usuario en CLI.
 */
fun main() {
    println("===========================================")
    println("    TORRES DE HANOI - Solución Recursiva")
    println("===========================================\n")

    print("Introduce el número de discos (recomendado 1-10): ")
    // Leer la respuesta del usuario desde la entrada estándar
    val respuesta = readLine()

    // Intentar convertir la entrada a un entero, manejar errores con un bloque `try-catch` o `toIntOrNull`
    val numDiscos = respuesta?.toIntOrNull()

    // Validación
    if (numDiscos == null || numDiscos < 1) {
        println("Error: El número de discos debe ser un número entero y al menos 1.")
        // Terminar la ejecución del programa
        exitProcess(1) 
    }

    // Advertencia para muchos movimientos
    if (numDiscos > 15) {
        val movimientos = (2.0.pow(numDiscos) - 1).toLong() // Usamos Long para números grandes
        println("Advertencia: Con $numDiscos discos habrá $movimientos movimientos.")

        print("¿Deseas continuar? (s/n): ")
        val confirmar = readLine()

        if (confirmar?.lowercase() != "s") {
            println("Programa terminado.")
            return
        }
    }

    ejecutarHanoi(numDiscos)
}

Free Pascal

program TorresDeHanoi;

uses
  SysUtils, Math; // SysUtils para StrToIntDef, Math para Power

// Declaración de la variable global para el contador de movimientos
var
  ContadorMovimientos: Int64 = 0; // Usamos Int64 para asegurar que no desborde con muchos discos

{
  Función recursiva para resolver el problema de las Torres de Hanói.

  @param N Número de discos a mover.
  @param Origen Torre de origen (A, B, C).
  @param Destino Torre de destino (A, B, C).
  @param Auxiliar Torre auxiliar (A, B, C).
}
procedure Hanoi(N: Integer; Origen, Destino, Auxiliar: Char);
begin
  // Caso base: si solo queda un disco, muévelo directamente
  if N = 1 then
  begin
    Inc(ContadorMovimientos); // Incrementa el contador global
    WriteLn('Movimiento ', ContadorMovimientos, ': Mover disco 1 de torre ', Origen, ' a torre ', Destino);
    Exit; // Termina la ejecución de la función actual
  end;

  // 1. Mover N-1 discos de Origen a Auxiliar usando Destino
  Hanoi(N - 1, Origen, Auxiliar, Destino);

  // 2. Mover el disco más grande (el disco N) de Origen a Destino
  Inc(ContadorMovimientos);
  WriteLn('Movimiento ', ContadorMovimientos, ': Mover disco ', N, ' de torre ', Origen, ' a torre ', Destino);

  // 3. Mover N-1 discos de Auxiliar a Destino usando Origen
  Hanoi(N - 1, Auxiliar, Destino, Origen);
end;

{
  Ejecuta la lógica principal del problema y muestra el resumen.

  @param NumDiscos El número de discos con el que ejecutar el juego.
}
procedure EjecutarHanoi(NumDiscos: Integer);
var
  MovimientosTeoricos: Int64;
begin
  // Mostrar información inicial
  WriteLn('');
  WriteLn('Estado inicial:');
  WriteLn('  Torre A: ', NumDiscos, ' disco(s)');
  WriteLn('  Torre B: vacia (auxiliar)');
  WriteLn('  Torre C: vacia (destino)');
  WriteLn('');

  WriteLn('Objetivo: Mover todos los discos de A a C');
  WriteLn('Reglas:');
  WriteLn('  1. Solo se puede mover un disco a la vez');
  WriteLn('  2. Un disco grande nunca sobre uno pequeño');
  WriteLn('');

  WriteLn('-------------------------------------------');
  WriteLn('Secuencia de movimientos:');
  WriteLn('-------------------------------------------');

  // Resolver las Torres de Hanói: Mover de 'A' a 'C' usando 'B'
  Hanoi(NumDiscos, 'A', 'C', 'B');

  // Calcular movimientos teóricos mínimos: 2^N - 1
  MovimientosTeoricos := Trunc(Power(2, NumDiscos)) - 1;

  // Mostrar resumen
  WriteLn('');
  WriteLn('===========================================');
  WriteLn('RESUMEN:');
  WriteLn('===========================================');
  WriteLn('Total de movimientos realizados: ', ContadorMovimientos);
  WriteLn('Movimientos mínimos teóricos:     ', MovimientosTeoricos);
  WriteLn('');
  WriteLn('Estado final:');
  WriteLn('  Torre A: vacia');
  WriteLn('  Torre B: vacia');
  WriteLn('  Torre C: ', NumDiscos, ' disco(s)');
  WriteLn('');
  WriteLn('¡Problema resuelto correctamente!');
  WriteLn('===========================================');
end;

{
  Función principal para la interacción con el usuario en CLI.
}
procedure Main;
var
  Respuesta: String;
  NumDiscos: Integer;
  Confirmar: String;
  Movimientos: Int64;
begin
  WriteLn('===========================================');
  WriteLn('    TORRES DE HANOI - Solución Recursiva');
  WriteLn('===========================================');
  WriteLn('');

  Write('Introduce el número de discos (recomendado 1-10): ');
  ReadLn(Respuesta);

  // Intentar convertir la respuesta a entero de forma segura
  NumDiscos := StrToIntDef(Respuesta, 0);

  // Validación
  if NumDiscos < 1 then
  begin
    WriteLn('Error: El número de discos debe ser un número entero y al menos 1.');
    Halt(1); // Terminar la ejecución
  end;

  // Advertencia para muchos movimientos
  if NumDiscos > 15 then
  begin
    Movimientos := Trunc(Power(2, NumDiscos)) - 1;
    WriteLn('Advertencia: Con ', NumDiscos, ' discos habrá ', Movimientos, ' movimientos.');

    Write('¿Deseas continuar? (s/n): ');
    ReadLn(Confirmar);

    if UpperCase(Confirmar) <> 'S' then
    begin
      WriteLn('Programa terminado.');
      Halt(0);
    end;
  end;

  // Reiniciar el contador de movimientos por si acaso
  ContadorMovimientos := 0; 
  EjecutarHanoi(NumDiscos);
end;

// Punto de entrada del programa
begin
  Main;
end.

Harbour / Clipper / XBase

// Variable global para el contador de movimientos
STATIC nContadorMovimientos := 0

// ----------------------------------------------------------------------

// Procedimiento recursivo para resolver el problema de las Torres de Hanói.
PROCEDURE Hanoi( nDiscos, cOrigen, cDestino, cAuxiliar )

    // El número de discos debe ser un entero
    LOCAL n := nDiscos

    // Caso base: si solo queda un disco, muévelo directamente
    IF n == 1
        nContadorMovimientos++
        ? "Movimiento", nContadorMovimientos, ": Mover disco 1 de torre", cOrigen, "a torre", cDestino
        RETURN
    ENDIF

    // 1. Mover n-1 discos de origen a auxiliar usando destino
    Hanoi( n - 1, cOrigen, cAuxiliar, cDestino )

    // 2. Mover el disco más grande (el disco n) de origen a destino
    nContadorMovimientos++
    ? "Movimiento", nContadorMovimientos, ": Mover disco", n, "de torre", cOrigen, "a torre", cDestino

    // 3. Mover n-1 discos de auxiliar a destino usando origen
    Hanoi( n - 1, cAuxiliar, cDestino, cOrigen )

RETURN

// ----------------------------------------------------------------------

// Procedimiento principal para ejecutar el juego y mostrar el resumen
PROCEDURE EjecutarHanoi( nNumDiscos )
    LOCAL nMovimientosTeoricos

    // Mostrar información inicial
    ? ""
    ? "Estado inicial:"
    ? "  Torre A:", nNumDiscos, "disco(s)"
    ? "  Torre B: vacia (auxiliar)"
    ? "  Torre C: vacia (destino)"
    ? ""

    ? "Objetivo: Mover todos los discos de A a C"
    // ... Mostrar reglas (omitidas por concisión, pero la lógica es la misma)

    ? "-------------------------------------------"
    ? "Secuencia de movimientos:"
    ? "-------------------------------------------"

    // Resolver las Torres de Hanói
    Hanoi( nNumDiscos, "A", "C", "B" )

    // Calcular movimientos teóricos mínimos: 2^n - 1
    // Harbour tiene una función de potencia similar a C/Pascal
    nMovimientosTeoricos := INT(Pow(2, nNumDiscos)) - 1

    // Mostrar resumen
    ? ""
    ? "==========================================="
    ? "RESUMEN:"
    ? "==========================================="
    ? "Total de movimientos realizados:", nContadorMovimientos
    ? "Movimientos minimos teoricos:   ", nMovimientosTeoricos
    // ... Mostrar estado final (omitido por concisión)
    ? "¡Problema resuelto correctamente!"
    ? "==========================================="

RETURN

// ----------------------------------------------------------------------

// Punto de entrada del programa
PROCEDURE Main()
    LOCAL cRespuesta, nNumDiscos, nMovimientos, cConfirmar

    // Configuración inicial de la consola para leer la entrada
    SET CONSOLE ON

    ? "==========================================="
    ? "    TORRES DE HANOI - Solucion Recursiva"
    ? "==========================================="
    ? ""

    // Leer la entrada del usuario (similar a 'READ' o 'INPUT' en otros xBase)
    cRespuesta := Space( 10 ) // Reserva espacio para la respuesta
    @ 5, 1 SAY "Introduce el numero de discos (recomendado 1-10): " GET cRespuesta
    READ

    // Convertir la respuesta a número
    nNumDiscos := VAL( ALLTRIM( cRespuesta ) )

    // Validación
    IF nNumDiscos < 1
        ? "Error: El numero de discos debe ser al menos 1."
        RETURN
    ENDIF

    // Advertencia para muchos movimientos
    IF nNumDiscos > 15
        nMovimientos := INT(Pow(2, nNumDiscos)) - 1
        ? "Advertencia: Con", nNumDiscos, "discos habra", nMovimientos, "movimientos."

        cConfirmar := Space( 1 )
        @ 7, 1 SAY "¿Deseas continuar? (s/n): " GET cConfirmar
        READ

        IF UPPER( cConfirmar ) <> 'S'
            ? "Programa terminado."
            RETURN
        ENDIF
    ENDIF

    nContadorMovimientos := 0 // Asegurar el reset
    EjecutarHanoi( nNumDiscos )

    // Pausar para ver el resultado si se ejecuta en una ventana
    INKEY(0) // Espera una pulsación de tecla

RETURN

El juego que no lo es: usos prácticos de las torres de Hanoi

Evidentemente se trata de un juego matemático y que ha sido usado para aprender recursividad y algoritmos en general, ¿desde siempre?, en la programación. Claro está también, que no solamente es para aprender, pues también se usa para dar solución a problemas en este mundo del desarrollo.

Y en consecuencia, nos encontramos con usos y aplicaciones en la vida real. Veamos algunos.

1. Resolución de problemas recursivos en programación y desarrollo

Tal y como ya he comentado, se usa mucho tanto en el aprendizaje como en la aplicación de la recursividad, pero eso es la base porque:

• La usamos en la pila de llamadas (call stack).
• Dividir problemas complejos en otros más pequeños, idénticos.
• Gran cantidad de algoritmos en realidad: listas enlazadas, árboles, grafos, ordenación, búsqueda binaria y un largo etcétera.

2. Planificación y optimización de movimientos secuenciales

Un algoritmo como éste, se presta especialmente en todo aquello donde sólo podemos mover un elemento a la vez, tenemos restricciones sobre cómo ordenar y mover cosas. Ejemplo:

• Reorganizar contenedores en un puerto. Evidentemente no podemos poner contenedores grandes sobre pequeños.
• Almacenamiento en depósitos, almacenes, bibliotecas, etc. En cualquiera de los casos, si no se almacenan siguiendo un orden determinado, puede ocurrir alguna catástrofe, sea esta más o menos pequeña.

3. Migración de datos entre sistemas con restricciones

Sirva como ejemplo cuando se mueven datos de un servidor a otro, hay pasos intermedios y existen reglas de validación como por ejemplo: migración de discos RAID sin pérdida de información o migración de tablas de una base de datos en proceso «legacy -> staging -> producción».

4. Automatización en robótica

Si estamos ante robots que tienen que manipular determinados objetos o realizar tareas concretas que requieran una secuencia, límites, controlar circunstancias, etc. Es, en consecuencia, una de las áreas donde todo esto se puede dar especialmente.

5. Sistemas de archivos y copias de seguridad

Estamos ante una de las áreas con mayor aplicación de recursividad y algoritmo «torres de Hanoi». Muchos sistemas de backup incremental y rotativo, como el clásico método “abuelo–padre–hijo” (Grandfather–Father–Son), siguen una estructura análoga a las Torres de Hanoi:

• La copia más antigua no se sobrescribe hasta que pasa una secuencia completa.
• Se rota según patrones recursivos del tipo 1, 2, 4, 8, etc.

6. Compresión de datos y optimización de algoritmos: «divide & conquer»

Consecuentemente, visto todo lo anterior, éste es un área con múltiples aplicaciones también:

• Compresión por bloques.
• Análisis recursivo de imágenes.
• Segmentación jerárquica de datos.
• Y en definitiva todo lo que implica descomponer un problema enorme, procesar esas partes más pequeñas y finalmente, reconstruir un resultado final.

Obviamente, dado que aplicamos las mismas ideas o algoritmo para resolver problemas que en el fondo tienen características comunes, pues existen muchas similitudes entre diferentes aplicaciones.

7. Pruebas de estrés en recursos recursivos

Es posible que pensemos que esto podríamos incluirlo en el punto 1 de ejemplos de uso práctico, pero en realidad sería, un uso práctico sobre una solución consecuencia del punto 1:

• Testear el comportamiento de stacks profundos.
• Simular casos de recursión pesada.
• Evaluar límites de memoria.

¿Y todo eso dónde se da? Pues en lenguajes interpretados, máquinas virtuales (como la JVM de Java) o, por ejemplo, sistemas con microcontroladores con pila limitada.

No cabe duda que estamos ante uno de los algoritmos «esenciales» en la programación, base además de muchos otros.

¡Hasta luego!

La torres de Hanoi son un deber dentro del mundo de los algoritmos y la programación. En consecuencia, su comprensión correcta nos afianza y da una excelente base, especialmente en lo que se refiere a la recursividad.

Espero que os sea muy útil este artículo y os ayude en el camino de aprendizaje de la programación. Nada más, un saludo y hasta otra.

👉 Explora más recursos en nuestro portal educativo para seguir mejorando el nivel de tus estudios sobre algoritmos.

🥇 Ayúdanos con una pequeña donación y conseguiremos ofrecer más contenidos gratuitos con más frecuencia. Gracias. 🥇 (Puedes cambiar la cantidad)